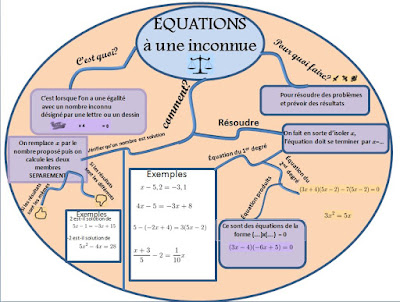
Pour réviser le brevet: quelques conseils
Découvrez les cours et définitions sous forme simplifiée pour une meilleure compréhension et mémorisation sur le modèle des cartes heuristiques ou mentales NOUVEAU: certaines cartes mentales sont expliquées par vidéo